Dropout Regularization With Tensorflow Keras
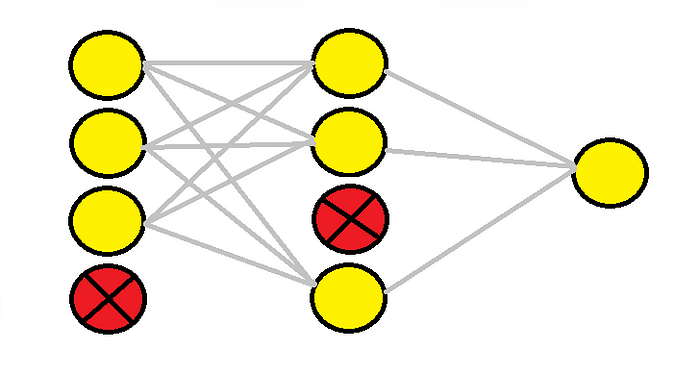
Deep neural networks are complex models which makes them much more prone to overfitting — especially when the dataset has few examples. Left unhandled, an overfit model would fail to generalize well to unseen instances. One solution to combat this occurrence is to apply regularization.
The technique we are going to be focusing on here is called Dropout. We will use different methods to implement it in Tensorflow Keras and evaluate how it improves our model.
“Dilution (also called Dropout or DropConnect) is a regularization technique for reducing overfitting in artificial neural networks by preventing complex co-adaptations on training data. It is an efficient way of performing model averaging with neural networks.”
— Wikipedia
The Mechanics of Dropout
Dropout is a computationally cheap and effective technique used to reduce overfitting in neural networks. The technique works by randomly dropping out selected neurons during the training phase. Neurons in later layers do not reap the contribution of dropped-out neurons during forward propagation, nor will updates be made to the dropped-out neurons during backpropagation.
“By dropping a unit out, we mean temporarily removing it from the network, along with all its incoming and outgoing connections”
— Srivastava, et al. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting
You can think of the dropout procedure as an ensemble method that trains several varying neural network architectures in parallel. The effect of dropping out neurons at random is that other neurons must intervene to make predictions for the absent neurons — this results in slightly different models being seen during the forward pass which makes the network less sensitive to specific weights of neurons.
Applying Dropout with Tensorflow Keras
Dropout is used during the training phase of model building — no values are dropped during inference. We simply provide a rate that sets the frequency of which input units are randomly set to 0 (dropped out). Next, we will explore various ways to use dropout with Tensorflow Keras.
I’ll be using the make_classification class from scikit-learn to generate a random binary classification dataset. The training dataset I’ll create will have 1000 instances and 20 features with 13 of them being informative. The testing dataset will contain 200 instances and 20 features with 13 of them being informative.
To define a baseline, we will build a three layer neural network (two hidden layers and an output layer): The first hidden layer will have 10 neurons, the second will have 10 neurons, and the output will have 1 neuron to classify the classes. Adam optimization will be used to optimize the model with a learning rate of 0.001.
See the code to create the baseline below:
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from mlxtend.plotting import plot_decision_regions
# create training data
X_train, y_train = make_classification(
n_samples=1000,
n_informative=13,
random_state=2022
)
# create testing data
X_test, y_test = make_classification(
n_samples=200,
n_informative=13,
random_state=2022
)
# build ANN
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation="sigmoid",
input_shape=(X_train.shape[1], ),
kernel_initializer="glorot_normal"),
tf.keras.layers.Dense(10, activation="sigmoid"),
tf.keras.layers.Dense(1, activation="sigmoid")
])
model.compile(optimizer="adam",
loss="binary_crossentropy",
metrics=["accuracy"])
history = model.fit(X_train,
y_train,
epochs=100,
validation_data=[X_test, y_test],
verbose=0)
# plot the model
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.title("Learning Rate = 0.001")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.legend()
plt.show()
The output of this code is:

Applying Dropout to the Input Layer
Srivastava et al., recommend dropout with a 20% rate to the input layer. We will implement this in the example below which means five inputs will be randomly dropped during each update cycle — formula 1 / (1-rate).
“[…] we can use max-norm regularization. This constrains the norm of the vector of incoming weights at each hidden unit to be bound by a constant c. Typical values of c range from 3 to 4.”
— Srivastava, et al. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting
Join 16,000 of your colleagues at Deep Learning Weekly for the latest products, acquisitions, technologies, deep-dives and more.
It’s also recommended to impose a constraint on the weights for each hidden layer by ensuring the maximum norm of the weights does not exceed three. We do this by setting the value in kernel_constraint.
Here’s how we build on our last model:
model = tf.keras.Sequential(
[
tf.keras.layers.Dropout(0.2, input_shape=(X_train.shape[1], )),
tf.keras.layers.Dense(10,
activation="sigmoid",
kernel_initializer="glorot_normal",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dense(10,
activation="sigmoid",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dense(1, activation="sigmoid")
])
model.compile(optimizer="adam",
loss="binary_crossentropy",
metrics=["accuracy"])
history = model.fit(X_train,
y_train,
epochs=100,
validation_data=[X_test, y_test],
verbose=0)
# plot the model
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.title("Learning Rate = 0.001")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.legend()
plt.show()
The output from the code above is as follows:
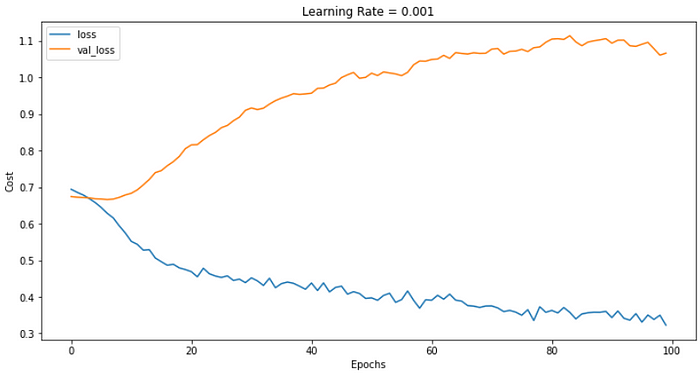
The plot above shows we’ve managed to reduce overfitting (notice the reduction of values on the Y-axis), but our model is still overfitting. Now, let’s apply dropout to the hidden layers.
Applying Dropout to the Hidden Layers
We may also decide to apply dropout to our hidden layers. Before we apply it to both input and hidden layers, we will take a look at the effects of applying it to the hidden layers.
“In the simplest case, each unit is retained with a fixed probability p independent of other units, where p can be chosen using a validation set or can simply be set at 0.5, which seems to be close to optimal for a wide range of networks and tasks.”
— Srivastava, et al. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting
The example below extends on our baseline model by adding dropout layers between layers 1–2 and 2–3. The dropout rate used is 0.5 with the same kernel constraint as seen in the example above.
# build ANN
model = tf.keras.Sequential(
[
tf.keras.layers.Dense(10,
activation="sigmoid",
input_shape=(X_train.shape[1], ),
kernel_initializer="glorot_normal",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(10,
activation="sigmoid",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(1, activation="sigmoid")
])
model.compile(optimizer="adam",
loss="binary_crossentropy",
metrics=["accuracy"])
history = model.fit(X_train,
y_train,
epochs=100,
validation_data=[X_test, y_test],
verbose=0)
# plot the model
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.title("Learning Rate = 0.001")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.legend()
plt.show()
The output of this code is as follows:
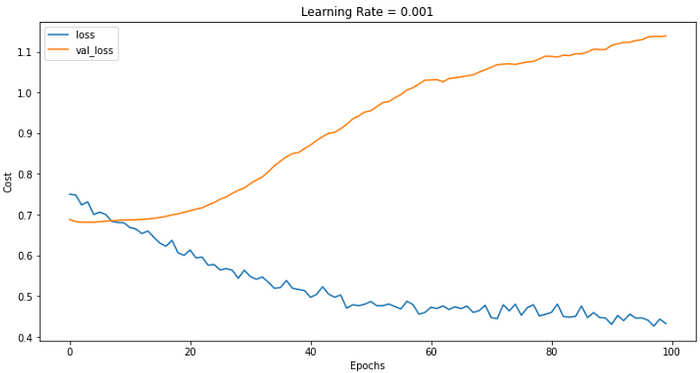
Once again, we were able to reduce overfitting in comparison to the baseline, but we are still overfitting the train data.
Applying Dropout to Input and Hidden Layers
In this section, we are going to apply dropout to both the input and dropout layers as follows:
# build ANN
model = tf.keras.Sequential(
[
tf.keras.layers.Dropout(0.2,
input_shape=(X_train.shape[1], )),
tf.keras.layers.Dense(10,
activation="sigmoid",
kernel_initializer="glorot_normal",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(10,
activation="sigmoid",
kernel_constraint=tf.keras.constraints.MaxNorm(3)),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(1, activation="sigmoid")
])
model.compile(optimizer="adam",
loss="binary_crossentropy",
metrics=["accuracy"])
history = model.fit(X_train,
y_train,
epochs=100,
validation_data=[X_test, y_test],
verbose=0)
# plot the model
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(history.history["loss"], label="loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.title("Learning Rate = 0.001")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.legend()
plt.show()
Which outputs:
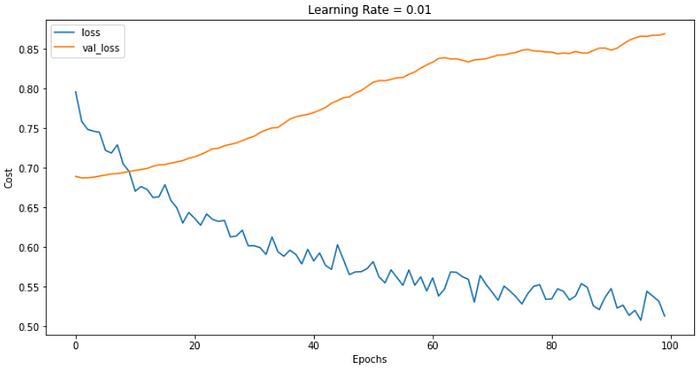
Overfitting has been reduced, but our model is still not performing as well as we would like. As a task for the reader, try to improve the loss of our model so it performs better on the validation data while reducing the amount of overfitting — the code can be found on GitHub.
Dropout is a powerful, yet computationally cheap regularization technique. In this article, you discovered the mechanics behind dropout, how to implement it on your input layers, and how to implement it on your hidden layers.
Recommended reads:
→ Deep Learning Tips & Tricks
→ A Gentle Introduction to Dropout for Regularizing Deep Neural Networks
→ Improving Neural Networks by Preventing Co-adaptation of Feature Detectors
→ Dropout: A Simple Way to Prevent Neural Networks from Overfitting